Theoretical Background

This section of the documentation will be dedicated to introducing you to the theoretical models that are used in TACO. We will start by introducing the formal definition of the system model,i.e., threshold automata and their properties with a simple example. Then, Section: Model Checking Algorithms gives you a high-level overview of the three model checking algorithms implemented in TACO.

Distributed Algorithms and the Byzantine Generals Problem¶

Before jumping into the model lets first take a look at what kinds of algorithms TACO has been designed for.

So let’s start with the question: What are distributed algorithms? In essence, a distributed algorithm is an algorithm designed to be executed by a group of computers, also called nodes, that can communicate over some kind of network. Such algorithms are, for example, vital to scaling modern applications across many servers, often across multiple data centers, or even across the globe.

However, the distributed setting is hard, or in the words of Lesslie Lamport:

A distributed system is one in which the failure of a computer you didn’t even know existed can render your own computer unusable. 19

One key challenge that makes the distributed setting hard, is that not all nodes necessarily agree on the current view of the system. For example, initially the nodes of the system might not agree on which nodes are part of the system. To get a number of nodes to agree, one needs to solve the challenge of consensus.

The consensus problem asks a set of nodes to agree on a data value by exchanging messages. Many protocols have been developed for achieving consensus, a famous example used in many systems is Raft 20. However, in a real world distributed setting failures or incorrect behavior must be expected. Unfortunately, failures are often not simple crash-stop failures.

To model more complex failure behavior, the model of “Byzantine Faults” or byzantine behavior has been developed 21. A byzantine fault allows a node to behave arbitrarily, it is allowed to follow the protocol and stop responding, or it can actively try to sabotage correct nodes.

Achieving consensus in such a setting is especially hard, or even impossible if there are more than $1/3 n$ faulty nodes where $n$ is the number of nodes 21.

In general most of the consensus algorithms rely on some form of voting. This is where TACOs internal model comes in.

Threshold Automata¶

This section introduces the underlying theoretical framework of TACO, which are (extended) threshold automata (TA) 4516.

Definition:

A threshold automaton (TA) 45 is a tuple $A=(L, \mI, \Shared, \Pi,\Rules, RC)$ where:

• $L$ is a finite set of locations.

• $\mI \subseteq L$ is the set of initial locations.

• $\Shared = \{x_0,\ldots,x_m\}$ is a finite set of shared variables over $\Nat_0$.

• $\Pi$ is a finite set of parameter variables over $\Nat_0$.

• $RC$, the resilience condition, is a linear integer arithmetic formula over parameter variables.

• $\Rules$ is a set of rules, where a rule is a tuple $r=(\from, \to, \varphi,\vup,\resets)$ such that:

  • $\from,\to \in L$.

  • $\varphi$ is a conjunction of lower guards and upper guards. A lower guard is a constraint $a_0 + \sum_{i=1}^{|\Pi|} a_i \cdot p_i \leq x$, with $x \in \Shared$, $a_0,\ldots,a_{|\Pi|} \in \mathbb{Q}$, $p_1,\ldots,p_{|\Pi|} \in \Pi$. An upper guard is a constraint $a_0 + \sum_{i=1}^{|\Pi|} a_i \cdot p_i > x$.
    The left-hand side of a lower or upper guard is called a threshold.

  • $\vup \in \Int^{|\Shared|}$ is an update vector for shared variables.

  • $\resets \subseteq \Shared$ is the set of shared variables to be reset to 0.

Most commonly, the parameter variables are $\Pi = \{n,t,f\}$, where $n$ is the number of processes, $t$ is a bound on the number of faulty processes, and $f$ is the actual number of faulty processes. This allows $RC$ to express assumptions about the fraction of faulty processes in the system, e.g., $RC = n > 3t\, \land\, t \geq f$.

If $\vup \in \Nat_0^{|\Shared|}$ and no variables are reset, then the TA is called a canonical TA (CTA). Otherwise we call it an extended TA (ETA)16.

Note that rechability is in general undecidable for ETA 1016. Consequently, TACO’s decision procedures become semi-decision procedures for the ETAs, which will in general not terminate when an ETA is safe.

Semantics¶

For a vector $\vp \in \Nat_0^{|\Pi|}$, we write $\vp \models RC$ if $RC$ holds after substituting parameter variables with values according to $\vp$. Then the set of admissible parameters is $\vP_{RC} = \{\vp \in \Nat_0^{|\Pi|} : \vp \models RC\}$.

Once a TA is specified, the number of processes to be modeled must also be defined through the function $\mN: \vP_{RC} \rightarrow \Nat_0$ (usually $\mN(n,t,f) = n - f$).

Configurations. A configuration of a TA is a triple $\sigma = (\vk, \vg, \vp)$, where $\vk \in \Nat_0^{|L|}$ assigns a number of processes to each location, $\vg \in \Nat_0^{|\Shared|}$ assigns a valuation to the shared variables, and $\vp \in \vP_{RC}$ assigns a valuation to the parameters. We say that a configuration is initial if $\vg = \vec{0}$ and $\forall i$ $\vk[i] > 0 \iff l_i \in \mI$.

Paths. A rule $r = (\from, \to, \varphi,\vup,\resets)$ is enabled in a configuration $\sigma = (\vk,\vg,\vp)$ if $\vec{k}[\from] > 0$ and $(\vg,\vp)$ satisfies the guard $\varphi$. In this case, we say that $r(\sigma) = (\vk',\vg',\vp')$ where $\vk'[\from]=\vk[\from] -1$, $\vk'[\to]=\vk[\to] + 1$, $\vg'=\vg + \vup$, and $\vp'=\vp$. A path $\pi$ is then a finite or infinite sequence of configurations $\pi = \sigma_0, \sigma_1, \ldots$ such that for each $i$ there exists an enabled rule $r_i$ with $\sigma_{i+1} = r_i(\sigma_i)$. We denote by $\Paths$ the set of all paths $\pi$ in the threshold automaton.

Example:

Figure 1 shows the pseudocode of a reliable broadcast, inspired by 22. In every round, processes with input $v=1$ will broadcast a message, then processes with $v=0$ will set $v=1$ if they received at least $t+1$ messages, and finally processes set $accept=true$ if at least $n-t$ messages have been received. If $accept$ is false at the end of the round, a new round starts.

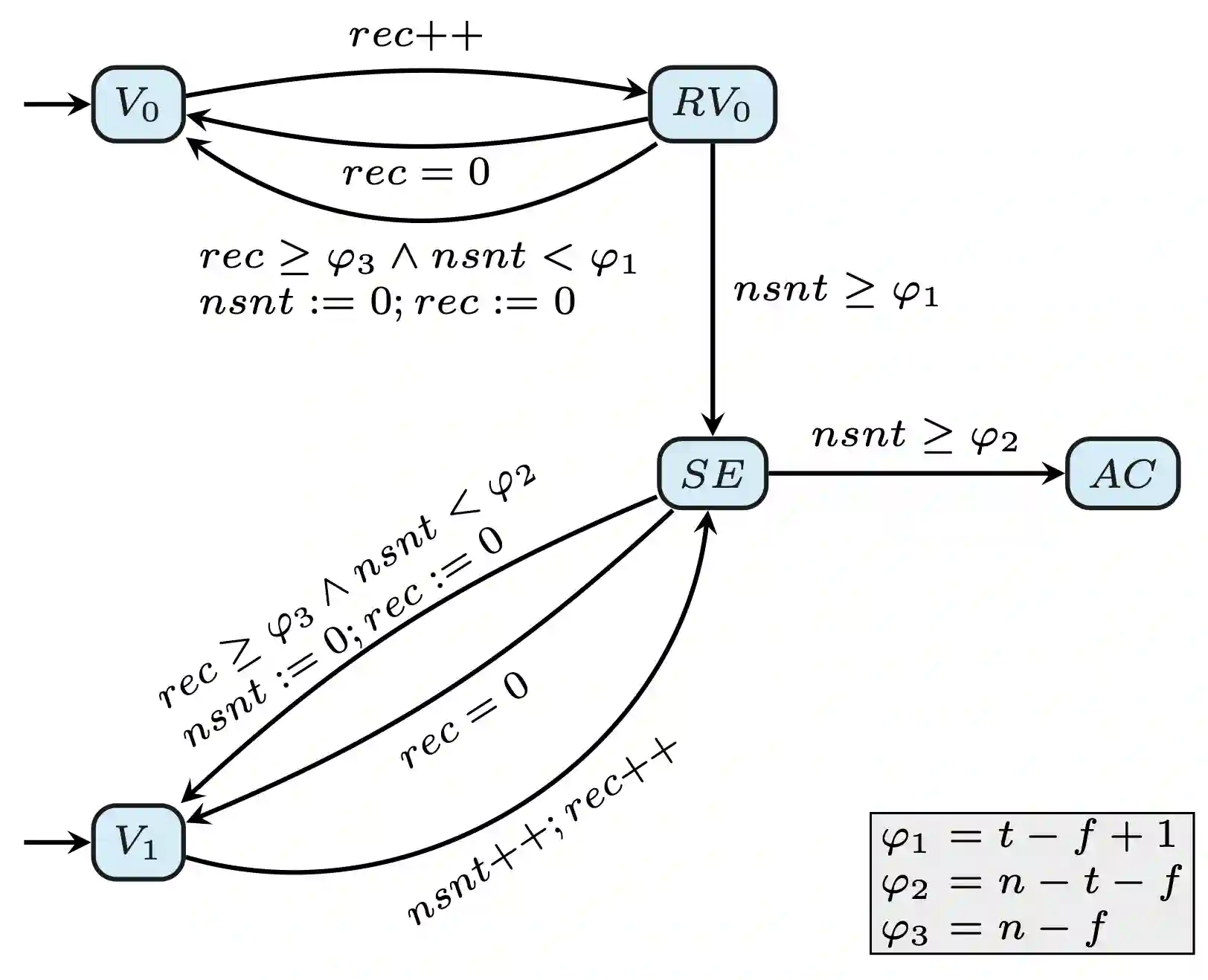
Example: Figure 2 depicts a TA for this algorithm, with $L = \{V_0, V_1, RV_0, SE, AC\}$, $\mI = \{V_0, V_1\}$, $\Shared = \{nsnt, rec\}$, $\Pi = \{n, t, f\}$, and $RC = n > 3t \land t \geq f \geq 0$. A process in $V_1$ has input 1 and can move freely (there is no guard) to $SE$, incrementing both variables $nsnt$ and $rec$ to simulate lines 4–6 of the algorithm. A process in location $V_0$ has input 0 and can move to $RV_0$, incrementing $rec$ to simulate line 6 (but not line 5, since the condition in line 4 evaluates to false). From $RV_0$, a process can move to $SE$ if $nsnt \geq \varphi_1$, simulating lines 7-8. Processes that started with $v=1$ already are in $SE$, corresponding to the fact that $v=1$ is not changed in line 8.

Note that instead of being $t+1$, $\varphi_1$ is chosen as $t + 1 - f$. This prevents processes from making a transition based on messages from faulty processes, hence the TA represents the behavior of correct processes and $f$ the effect of faulty processes on correct ones. For more details on the role of $f$, see 12.

Processes in $SE$ can move to $AC$ if $nsnt \geq \varphi_2$, simulating lines 9-10. If $nsnt < \varphi_2$ and $rec \geq \phi_3$ (this constraint corresponds to waiting long enough for all non-faulty processes to receive all messages), the condition in line 9 was not satisfied and a new iteration of the while-loop is started by moving back from $SE$ to $V_1$. The first process taking this transition will reset $nsnt$ and $rec$, the others take the transition that does not change any variables. Similarly, processes in $RV_0$ will move to $V_0$ to start the new round.

The $RC$ condition is critical here to ensure fault-tolerance: if $f > t$, then $AC$ will be reachable even if all processes start in $V_0$, violating the validity property.

Specifications on Threshold Automata¶

Basic Specifications¶

We consider two basic kinds of specifications: coverability, which refers to the notion of coverability that is widely used in parametrized verification, e.g., Petri nets 23 or VASS 24, and reachability.

Definition: The parametrized coverability problem is: Given a TA and a coverability specification $\vec{c} \in \Nat_0^{|L|}$, decide if there is a reachable configuration $\conf_r$^[1] with $\conf_r.\vk[i] \geq \vec{c}[i]$ for all $0 \leq i \leq |L|-1$.

Definition: The parametrized reachability problem is: Given a TA and a reachability specification $\vec{c_r} \in \Nat_0^{|L|}$, decide if there is a reachable configuration $\conf_r$ with $\conf_r.\vk[i] \geq \vec{c_r}[i] \land \left( \conf_r.\vk[i] = 0 \iff \vec{c_r}[i] = 0 \right)$ for all $0 \leq i \leq |L|-1$.

Usually, our specifications are definitions of error configurations, and therefore paths that reach them are called error paths.

$ELTL_{FT}$¶

TACO supports safety specifications in the fragment of $ELTL_{FT}$ 725 that can be translated into reachability or coverability properties. Formally, the syntax we support is defined as follows:

where $\varphi$ is a guard as defined in Threshold Automata and $Locs \subseteq L$.

Furthermore, TACO also supports lower integer bounds on the number of processes in a specific location. The extended $\mathsf{cform}$ syntax is:

where $l \in L, n \in \mathbb{N}$ and $* \in \{>, \geq\}$.

Example: One important property for consensus-based distributed algorithms is to check for validity, i.e., if no process received a specific value (e.g., 0), then no process should decide on that value. 1 specifies the valdity property in $ELTL_{FT}$ as follows:

To check if this property holds, TACO transforms this formula into a coverability specification that requires at least one process to be eventually in location $AC$ while all correct processes initially start in location $V1$. If such a configuration is reachable, then the validity property is violated. Otherwise the property holds.

For further reading on the model of threshold automata, we refer the reader to 123456781713141516.

The next section Model Checking Algorithms will introduce the model-checking algorithms implemented in TACO.