In TACO, we implemented three algorithms for model checking safety properties in threshold-based fault-tolerant distributed protocols. The first two algorithms, one based on well-structured transition systems (WSTS) and the other a symbolic algorithm using binary decision diagrams (BDDs), were originally introduced in 1. In addition, we provide the first publicly available implementation of the SMT-based reachability algorithm proposed in 2. While the authors of 2 reported an implementation and experimental results, their prototype has not been released. In the following, we present a high-level overview of these algorithms and refer the reader to the respective publications for further details.
SMT Model Checking Algorithm¶
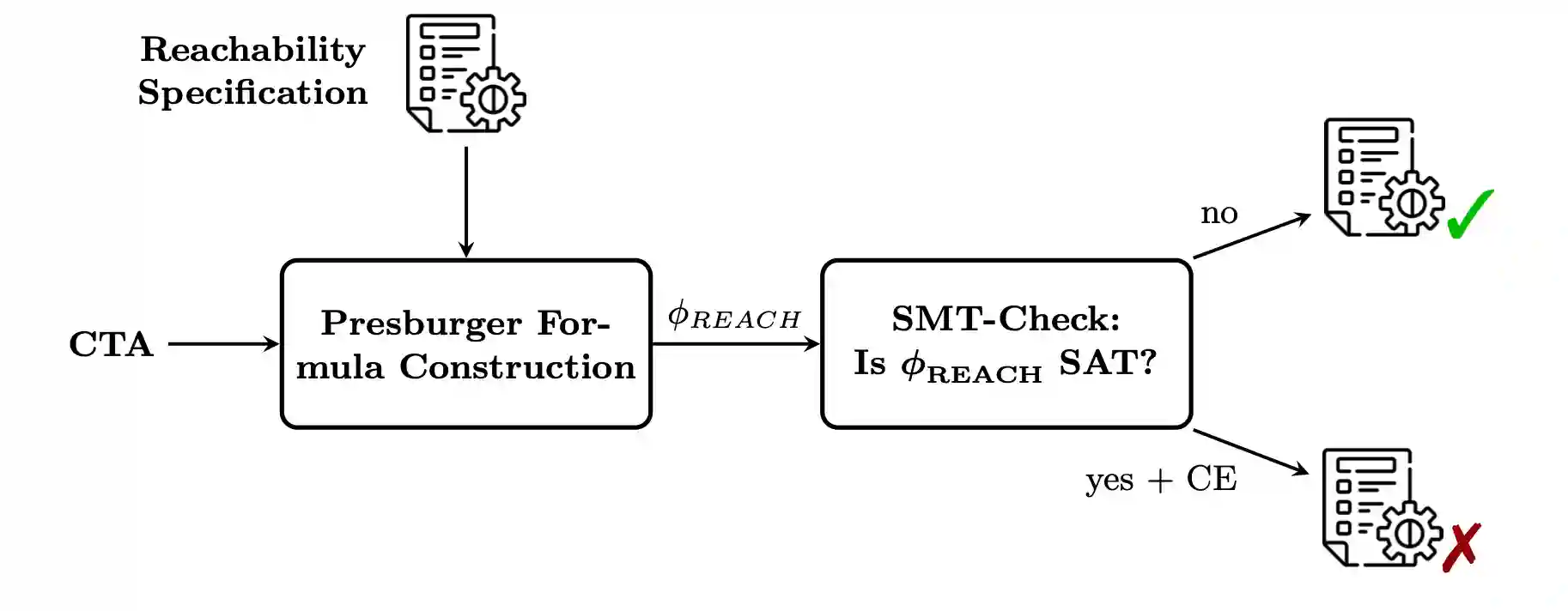
Figure 1:Architecture of the SMT-based model checking algorithm.
Balasubramanian et al. 2 showed that the reachability problem for MTA can be reduced to deciding the satisfiability of an SMT formula. More precisely, they construct an existential Presburger arithmetic formula such that holds if and only if is reachable from for the given MTA.
A central notion in this construction is the context of a configuration , defined as the set of lower guards that evaluate to true together with the upper guards that evaluate to false. A MTA path is called steady if all its configurations have the same context. The key idea underlying the SMT-based approach is that any MTA execution with guards can be represented as the concatenation of at most steady paths 2. Therefore, for each steady path, the formula encodes several constraints: the number of times each rule is fired, the effect on the number of processes in each location, the changes to shared variables, and that each fired rule is reachable via a sequence of rules where the target location of one rule provides the source location required to fire the next, starting from a location that initially contains a process ( “firable” chain of rules). Additional base constraints ensure that parameters, total process counts, and the guard context remain consistent along the path. Formally, the construction yields:
where is a polynomial sized existential Presburger formula such that is true iff can be reached from by firing at most one rule.
Note that the above construction may produce formulas of exponential size due to the exponential number of possible rule chains (see 2 for details).
Implementation Details. This algorithm uses the basic TA representation, shown as LIATA in Figure 1.
In contrast to the original implementation of the approach 2, we do not use non-deterministic guessing to keep SMT queries small. Instead, we encode all steady paths and leave it to the SMT solver to resolve the non-determinism.
Usage. To use the SMT model checking algorithm with TACO, the user needs to specify the option smt when invoking the tool from the command line.
ACS Model Checking Algorithm¶
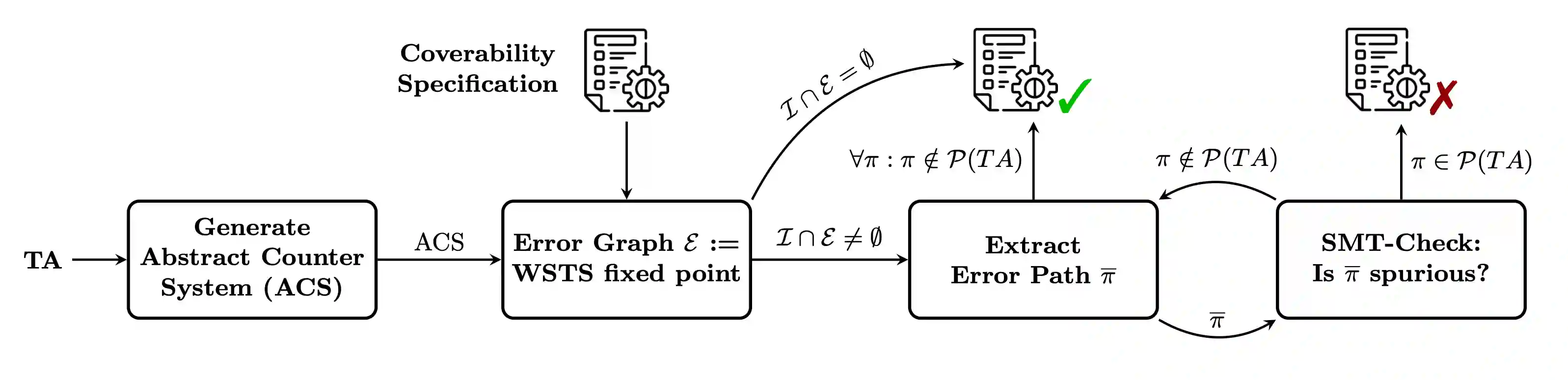
Figure 2:Workflow of the ACS model checking algorithm.
Given a TA, the algorithm begins by abstracting it into an IntervalTA, and then constructs an abstract counter system (ACS) which models its semantics for an arbitrary number of processes.
The IntervalTA is similar in structure to the original TA, but shared variables are mapped to a finite domain through parametric interval abstraction. A parametric interval is defined by the thresholds in the TA that may include parameters. This abstraction preserves sufficient information about variable valuations to evaluate the guards of all rules in the TA.
Then, an ACS is a formal model such that a configuration of the ACS specifies the current number of processes in all locations and the current abstract values (within the finite domain of parametric intervals) of the shared variables. It was shown in 1 that an ACS forms a WSTS, which allows infinite sets of ACS configurations to be represented using finite sets, called minimal bases. Furthermore, given an infinite set of configurations represented by its minimal basis, one can effectively compute a minimal basis that represents the infinite set of all configurations that can reach .
Therefore, given a TA and a coverability specification , the algorithm generates an ACS and computes the fixed point of all configurations that can reach . If the fixed point does not include an initial configuration, the TA is deemed correct and we terminate. Otherwise, an error graph is constructed, representing all abstract paths from an initial configuration to an error configuration.
However, these abstract paths can be spurious, for example, transitions between parametric intervals might occur unrealistically fast. Every such is therefore checked using an SMT solver to determine whether it can be instantiated to a concrete error path . If such a is found, the TA is incorrect and the algorithm terminates. If all abstract paths are spurious, then no concrete error paths exists and the TA is correct. Note that the error graph may also be empty, in which case the algorithm can immediately terminate and conclude correctness.
When the input is an ETA, this algorithm becomes a semi-decision procedure: it may fail to terminate if the ETA is correct. Note that this algorithm does not support reachability specifications, as the well-quasi order (wqo) of our WSTS is not suitable for representing the sets defined by a reachability specification.
Implementation Details. At the implementation level, the input received (after preprocessing) is internally called a linear integer arithmetic TA (LIATA). It corresponds directly to the TA defined in Threshold Automata. As depicted in Figure 1, to use it in this algorithm it is translated into an ACSTA in two steps:
To implement the interval abstraction mentioned above, we need a total ordering between thresholds that contain parameters. may constrain the possible orders between the thresholds, but in general we start from a partial order and need to consider all its completions. We use the SMT solver to compute all possible orders under and construct the corresponding IntervalTA for each of them. To prove correctness of the original TA, all of these IntervalTA need to be checked.
In the implementation of the ACS state space exploration, each configuration is represented as a vector of integers (where an entry either represents the number of processes is some location, or the interval for the valuation of one shared variable). To facilitate this, an IntervalTA is amended with mappings from shared variables and locations to indices of this configuration vector.
To efficiently implement the WSTS-based fixed point computation, a minimal basis of all visited configurations is maintained in a tree data structure, facilitating fast lookups of comparable configurations (with respect to the wqo). This is especially important as we only insert a newly visited configuration if no comparable configuration has been explored.
As a heuristic that has proven useful, the SMT checks for spuriosity of abstract error paths are done incrementally over the length of the path. This allows us to exclude whole sets of abstract paths with relatively simple SMT queries, and the SMT solver can reuse information from the shorter paths when checking their extensions. However, the performance of this heuristic depends on how efficiently the SMT solver supports incremental queries.
Usage. To use the ACS model checking algorithm with TACO, the user needs to specify the option acs when invoking the tool from the command line.
ZCS Model Checking Algorithm¶
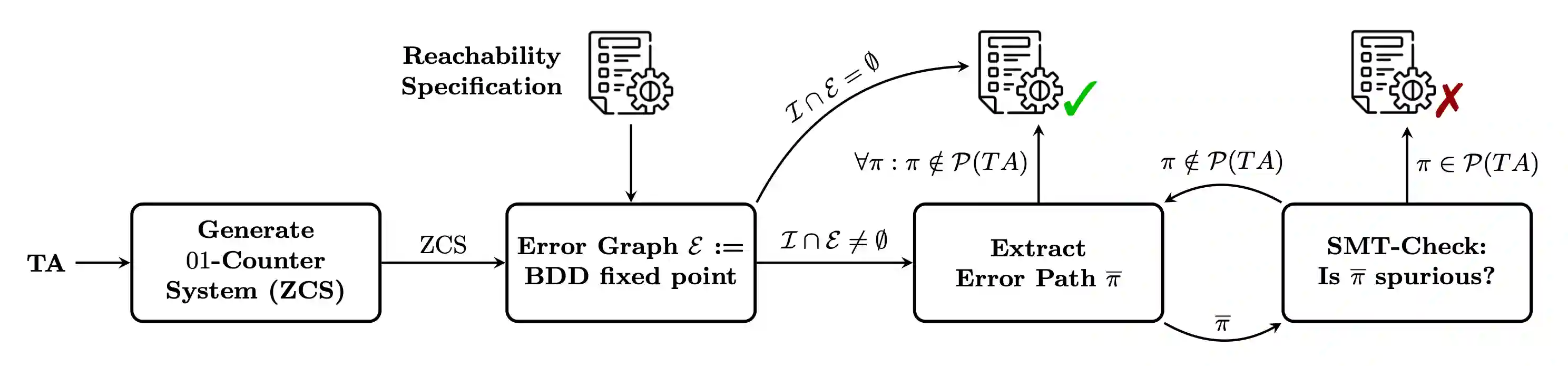
Workflow of the ZCS model checking algorithm.
The algorithm follows a workflow similar to the ACS-based approach in ACS Model Checking Algorithm but operates over a different abstract model, the 01-counter system (ZCS). A ZCS can be seen as a further abstraction of the abstract counter system, where integer counters are replaced by binary counters. That is, if the counter of location is set to 1, this indicates that one or more processes reside in . This abstraction has two important consequences. First, the ZCS is a finite-state model, as each counter takes only two values. Second, the finite state space can be represented compactly and manipulated efficiently using Binary Decision Diagrams (BDDs) 3. Therefore, given a TA and a reachability specification, the ZCS algorithm first constructs the corresponding ATA, then creates the ZCS and the set of ZCS error configurations defined by the specification. Since a ZCS is finite-state, we perform a BDD-based backward exploration from the error configurations until reaching a fixed point. If no initial configuration is included in the fixed point, the TA is deemed correct. If an initial configuration is reached, an error graph is generated that encodes all potential paths from an initial configuration to an error configuration.
As in the ACS-based approach, the abstraction may introduce spurious error paths. To eliminate them, each abstract path in the error graph is checked using an SMT solver. If a concrete error path is discovered, the TA is declared incorrect. Otherwise all abstract paths are spurious and the TA is correct. For ETAs, the procedure is only a semi-decision procedure.
Implementation Details. As an input, this algorithm uses a set of IntervalTA (see Figure 1), as explained in the implementation details of ACS Model Checking Algorithm.
As a heuristic, a variant of this algorithm can also be used to check only whether the error graph is empty. This requires less bookkeeping than in the standard algorithm and allows it to terminate even faster (at the cost of only giving a definitive answer about correctness if the error graph really is empty).
If an error graph is constructed, then spuriosity checks are done breadth-first, i.e., starting with the shortest paths from initial states to error states.
Usage. To use the ZCS model checking algorithm with TACO, the user needs to specify the option zcs when invoking the tool from the command line. Additionally, the user can choose a heuristic for exploring the error graph depending on the input TA by specifying the option –heuristic. Since TACO automatically detects whether the input TA is a MTA or an ETA, this flag does not need to be set by the user to choose a suitable heuristic. However, if the user wants to check only whether the error graph is empty, they can set the flag to empty-error-graph-heuristic.
- Baumeister, T., Eichler, P., Jacobs, S., Sakr, M., & Völp, M. (2024). Parameterized Verification of Round-Based Distributed Algorithms via Extended Threshold Automata. In A. Platzer, K. Y. Rozier, M. Pradella, & M. Rossi (Eds.), Formal Methods - 26th International Symposium, FM 2024, Milan, Italy, September 9-13, 2024, Proceedings, Part I (Vol. 14933, pp. 638–657). Springer. 10.1007/978-3-031-71162-6_33
- Balasubramanian, A. R., Esparza, J., & Lazic, M. (2020). Complexity of Verification and Synthesis of Threshold Automata. In D. V. Hung & O. Sokolsky (Eds.), Automated Technology for Verification and Analysis - 18th International Symposium, ATVA 2020, Hanoi, Vietnam, October 19-23, 2020, Proceedings (Vol. 12302, pp. 144–160). Springer. 10.1007/978-3-030-59152-6_8
- Akers. (1978). Binary decision diagrams. IEEE Transactions on Computers, 100(6), 509–516.